Macroscopic quantum tunneling wins 2025’s Nobel Prize in physics

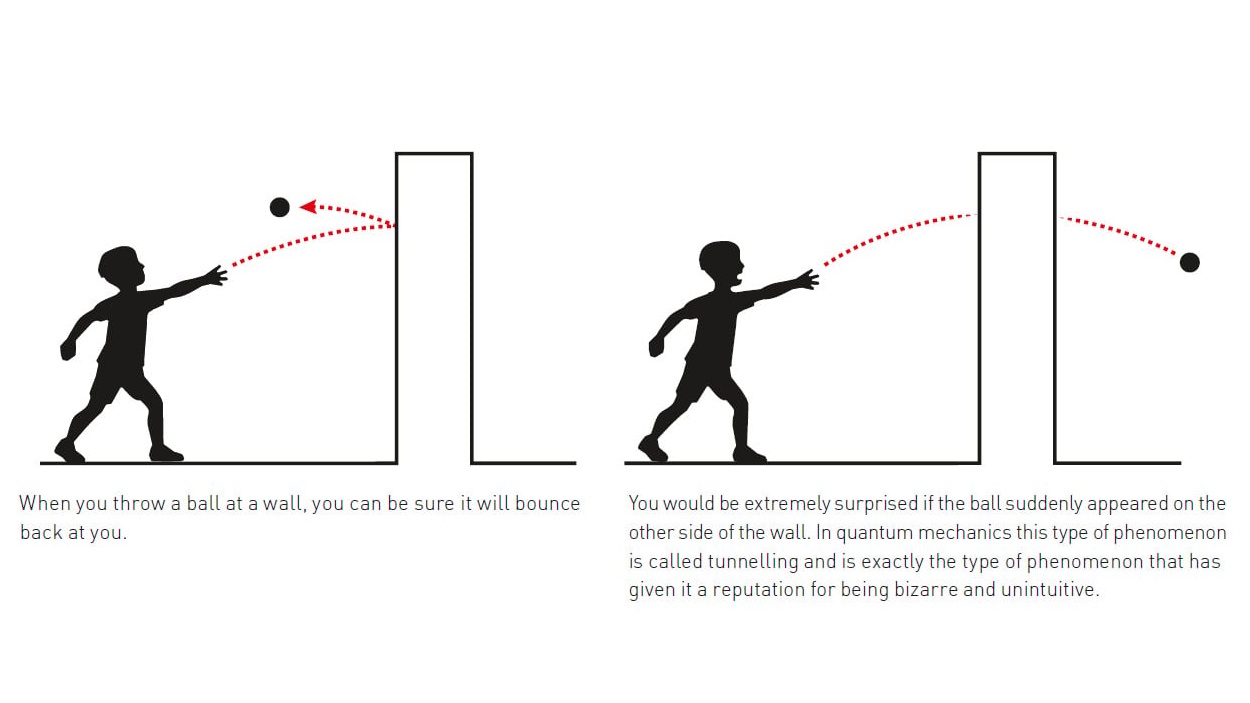
Here in the classical world, if you throw a ball against a solid wall, that wall will be impenetrable, and the ball will bounce right back. Do it a hundred times, a thousand times, a million times, and the result will always be the same. As long as the wall remains intact, the ball will always remain on that same, initial side of the wall.

Things are a little different in the quantum world, however. If you fire a subatomic particle, like an electron, at a barrier — whether that’s a solid barrier made of atoms or merely an energy barrier, where the particle doesn’t have enough energy, itself, to get to the other side — most of the electrons will bounce back. But there’s a chance, dependent on the:

• speed and energy of the electron,
• the height and thickness of the (physical or energy) barrier,
• and the rules of quantum physics,

that the electron won’t bounce back, but instead will tunnel through to the other side.

For a long time, many thought that this type of quantum phenomenon would only be important on tiny, microscopic scales. But with the right setup, quantum tunneling can be observed in macroscopic systems, including in electronic circuits. This enables not just large-scale observations of inherently quantum effects, but the ability to create a new kind of computer: a quantum computer. Here’s how that research, pioneered more than 40 years ago, has led to new frontiers in modern physics, as well as 2025’s Nobel Prize in physics.

When a ball begins at the top of a hill and is released, it will roll down to a low point, often coming to rest in the “true minimum” state of the lowest possible valley, but at other times, coming to rest in a false minimum, or a state from which it does not have enough energy to escape from into a still-lower energy state. In the classical world, you must overcome the barrier of the walls around your valley. But in the quantum world, quantum tunneling allows a different path for escape.

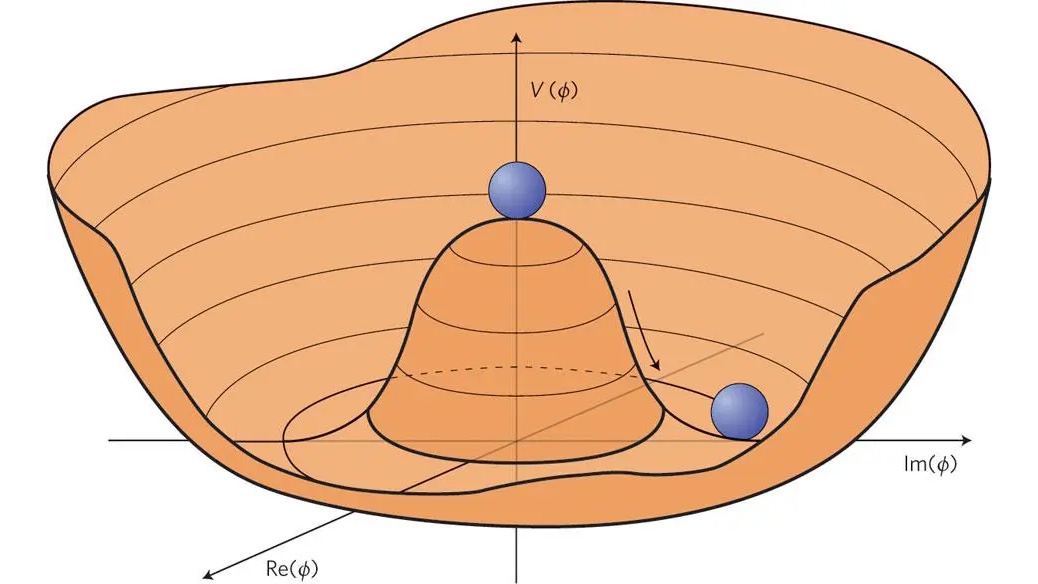
In several scientific fields, such as physics and chemistry, we often visualize the idea of being in a particular “energy state” as existing in a single valley amidst a series of peaks and valleys. If you begin with a ball at the top of a hill and let it go, the ball will roll down the hill, gaining energy and speed, typically over bumps or around obstacles, and then losing speed when it encounters a flat area, often coming to rest within a valley. This doesn’t just happen for balls rolling down hills, but for rain that pools into puddles, ponds, and lakes, for molecules that fold into a particular configuration, and even for electrons that cascade down into a stable or quasi-stable energy state.

From a classical perspective, coming to rest in this valley — whether it’s a physical valley or merely an energy valley — the way to escape is clear: you have to give whatever’s caught in that valley an energetic kick. That kick could come from mechanical, electrical, or chemical energy, but the only way to get out of the valley is to get your system out of that “stuck” configuration: whether it’s a ball stuck in a valley, a molecule stuck in a non-ideal configuration, or an electron stuck in a state that isn’t the true ground state of a system. Classically, if you don’t have (or don’t receive) enough energy to get over the lowest lip of whatever valley you’re stuck in, you’re doomed to remain there.

In many physical instances, you can find yourself trapped in a local, false minimum, unable to reach the lowest-energy state, which is known as the true minimum. Whether you receive a kick to hurdle the barrier, which can occur classically, or whether you take the purely quantum mechanical path of quantum tunneling, going from one state to another is always possible so long as no fundamental conservation laws are violated. This is an example of a first-order phase transition, rather than a smooth (second-order) transition without any false minima.

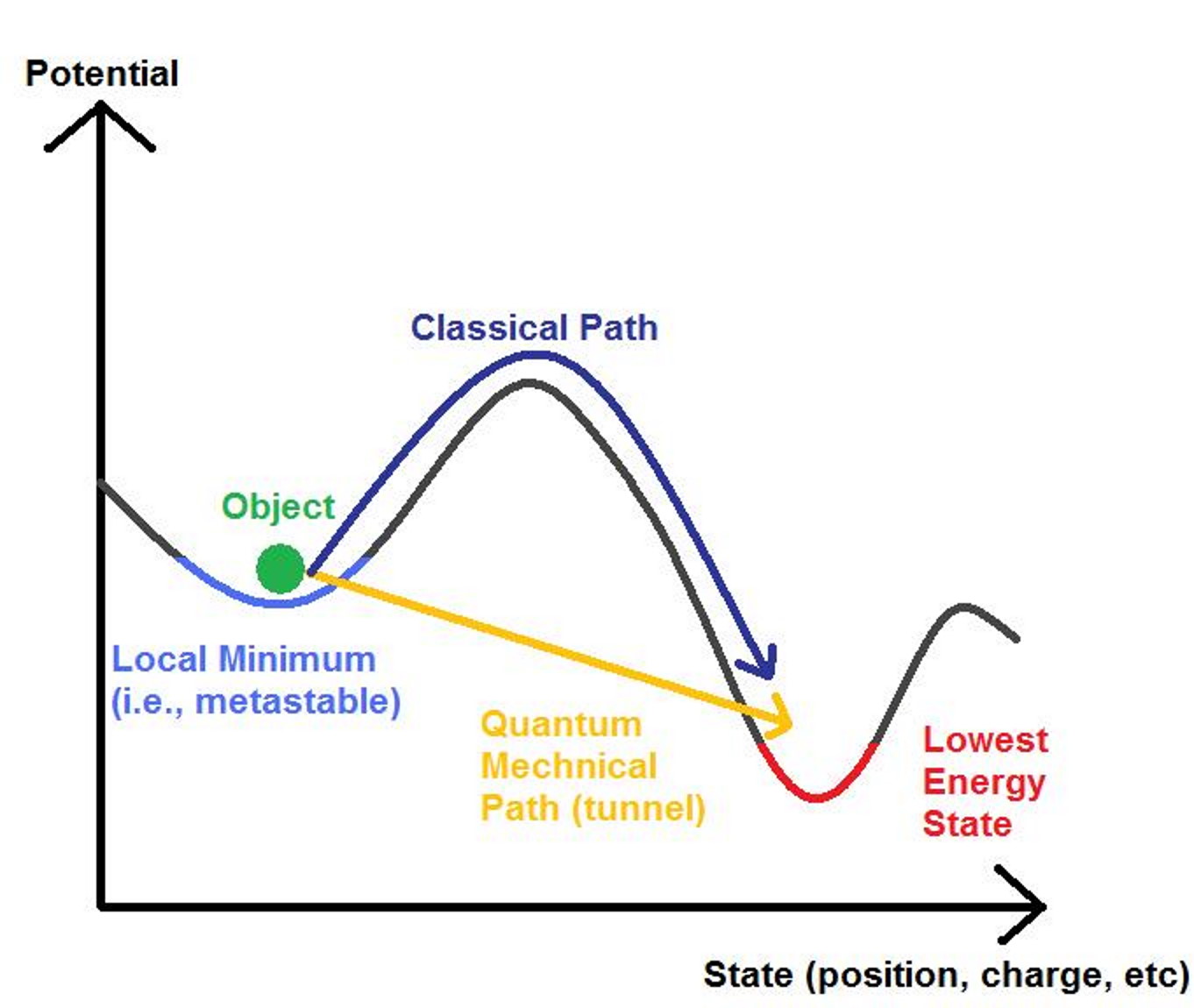
But in quantum physics, there’s another way out. These things that we think of as “balls” or “molecules” or “electrons,” from a classical perspective, always behave as particles: entities with fixed and well-determined positions and momenta at any moment in time. Part of the quantum revolution of the early 20th century, however, was the recognition that even something as straightforward as the position of a quantum entity wasn’t well-described by a single exact value, but rather by an extended probability distribution that’s better described by wave-like behavior.

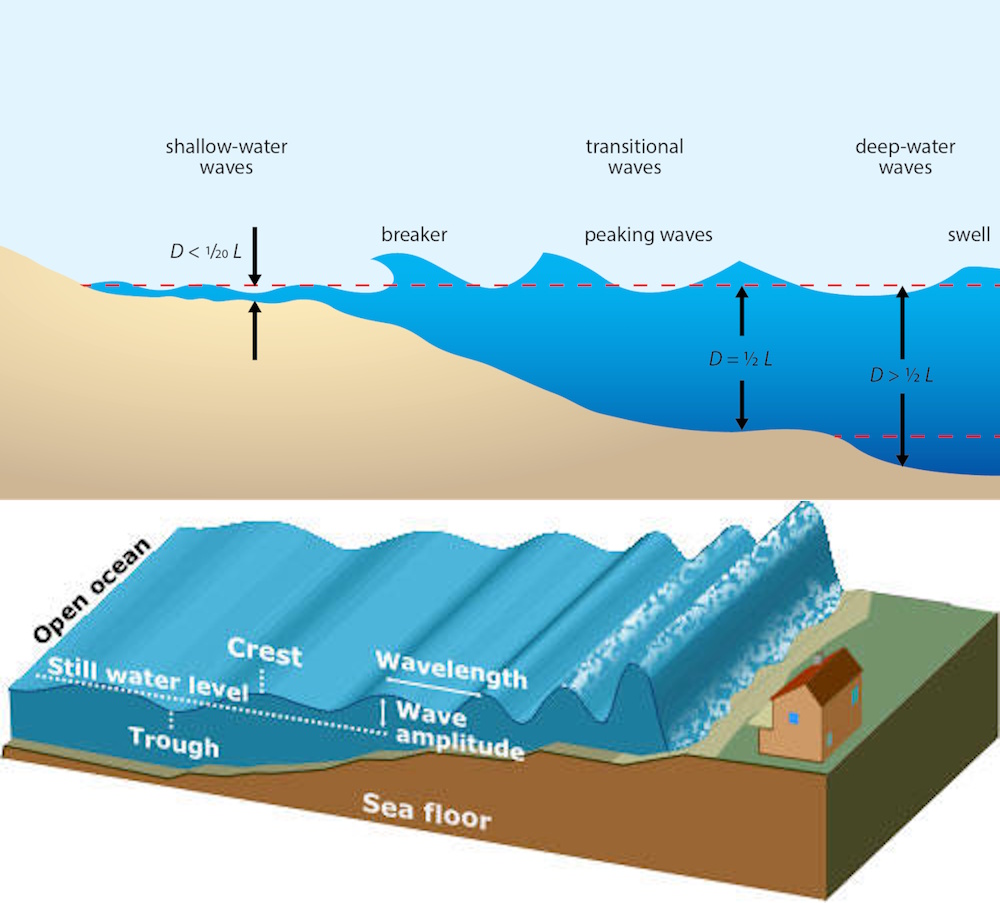
The idea of waves propagating through a barrier has been around for a long time, since before the existence of quantum mechanics. In fact, the study of wave-like phenomena can be traced back to early experiments done in the 1600s with water waves by pioneers like Christiaan Huygens, who understood that all waves could be treated as superpositions of many circular waves, propagating outward, all together. If you took a plane wave — a “straight-line” wave — in a shallow pool of water, the wave crests would be large, high, and tightly bunched together: appearing as a large-amplitude wave. If you then dramatically changed the water’s depth level, increasing it substantially, it would look like the wave disappeared entirely, as the height dropped and wavelength increased.

However, in reality, a fraction of that wave’s original energy continues propagating even through the “barrier” of the ultra-deep water. When the wave arrives in shallow waters once again, the wave behavior would reappear, potentially leading to crashing, large-amplitude waves on shore.

A water wave that propagates from shallow to deep water will appear to shift to lower wave amplitudes, longer wavelengths, and a stiller, steadier water surface. However, the wave continues to propagate even through those deep waters, and when it arrives at shallow waters again, those waves build up, rise to higher amplitudes, narrow to shorter wave spacings, and create breaking, crashing waves or, in an extreme scenario, even a tsunami.

The idea of a quantum wavefunction was only formalized into quantum mechanics in 1926, however, with the advent of the Schrödinger equation. Just a year later, quantum physicist Friedrich Hund applied the equation to a particle in a valley: a false minimum. When that particle — now described by a wavefunction — encountered the barrier representing the high walls on the edge of the valley, the most common behavior, with the largest probability, was the “bounce-back” behavior that was the hallmark of the classical case. However, there was a small but significant, non-zero chance that the particle would propagate through that barrier, emerging out the other side: marking the origin of the phenomenon we now know as quantum tunneling.

Just as the “deep water” doesn’t completely drive even a small-amplitude wave that starts in shallow waters to extinction, a barrier doesn’t drive the probability of a particle’s position outside of whatever valley it gets caught in to zero: even on the other side of the barrier. Before 1930 rolled around, tunneling was independently discovered again by Mandelstam and Leontowitsch, and a class of radioactive decays (alpha decay) of atoms was able to have their half-life explained through the mathematical probability of quantum tunneling to the decayed state: work done by George Gamow and, independently, by Gurney and Condon.

This animation shows a simulation of a wave packet, traveling rightward, as it strikes a high but thin potential energy barrier. The solution is described by the time-dependent Schrödinger equation, which shows most of the wave packet’s probability function being reflected, but a small fraction of it being transmitted to the other side of the barrier, showcasing the phenomenon of quantum tunneling.

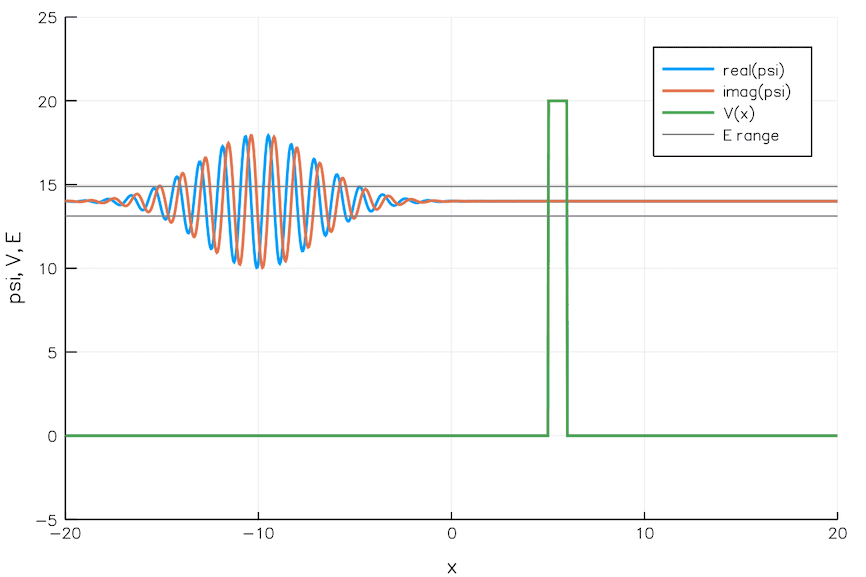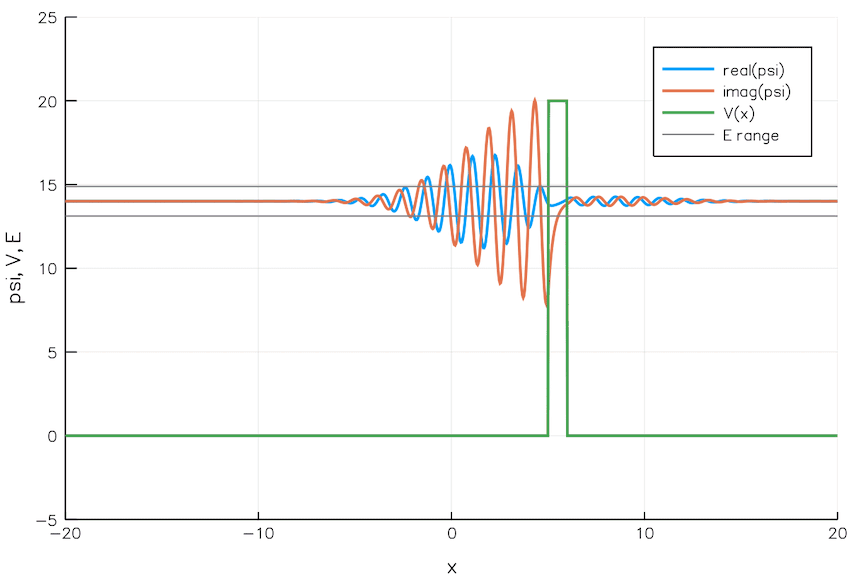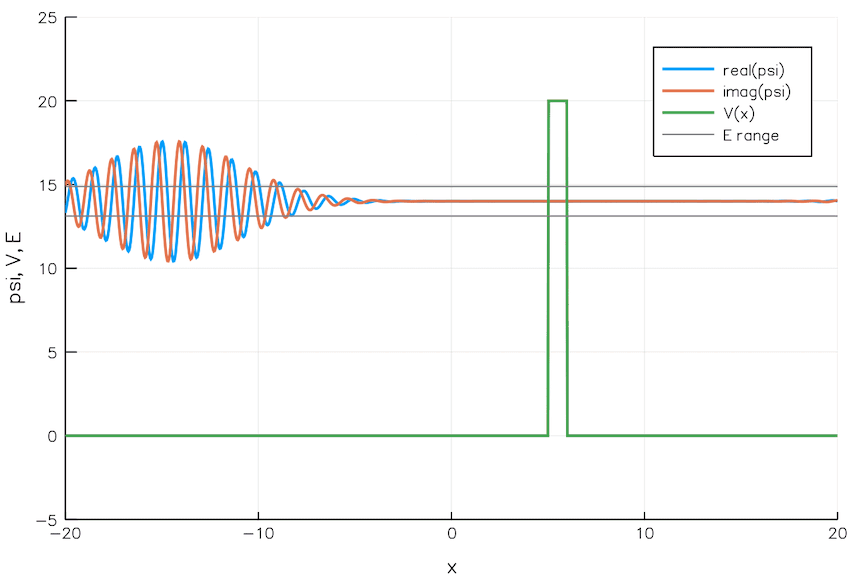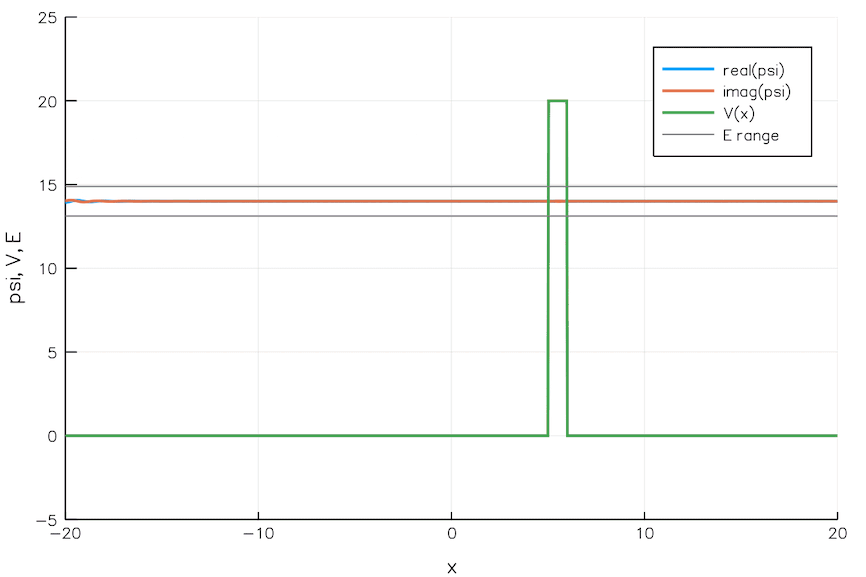
Quantum systems, indeed, weren’t confined to the classical behavior one would come to traditionally expect, but instead could spontaneously transition to a final state — one that overcomes the barriers that would prevent them from getting there classically — through this inherently quantum phenomenon of tunneling. However, the ability to quantum tunnel was typically restricted to particles that didn’t interact with other particles or their environments. If you kept interacting with (or watching) a particle in a false-minimum state, or a “valley” in the classical sense, it would never tunnel at all: a phenomenon known as the quantum version of Zeno’s paradox.

It was generally thought, then, that quantum tunneling would only be workable on these tiny, microscopic scales, and that this phenomenon would be impossible to realize on macroscopic scales. For nearly 60 years after we stumbled upon our earliest understanding of quantum tunneling, this proved to indeed be the case. But all of that changed with a series of experiments in 1984 and 1985, conducted by three scientists working at UC Berkeley:

• John Clarke, a professor and immigrant from the United Kingdom whose lab it was,
• Michel H. Devoret, his then-postdoctoral fellow who immigrated to the United States from France,
• and John M. Martinis, his graduate student from the United States.

It is this trio, after all, and their pioneering work, that was awarded the 2025 Nobel Prize in physics.

The 2025 Nobel Prize in physics was awarded to John Clarke, Michel Devoret, and John Martinis, for “the discovery of macroscopic quantum mechanical tunnelling and energy quantisation in an electric circuit.” Their work has led to profound applications in the decades since.

The key was to leverage another inherently quantum phenomenon: that of superconductivity, to create an electronic circuit that could conduct an electric current with no resistance at all. For most conducting materials, the resistance drops as you lower the temperature in a steady, predictable fashion. But then, for some materials, when you drop below a critical temperature, the resistance all of a sudden plummets all the way to zero: achieving a state of superconductivity. While some research focuses on identifying different properties of superconducting materials and different states of superconductivity, Clarke’s team focused on combining the unique properties of a superconductor with the phenomenon of quantum tunneling to create a macroscopic electronic circuit that exhibited inherently quantum behavior.

The key was to leverage a setup known as a Josephson junction, pioneered by Nobel Laureate Brian Josephson back in 1962. Just as charged particles moving through a conductor (i.e., an electrical current) can induce currents and magnetic fields in surrounding materials, so too can electric currents within a superconductor induce electromagnetic phenomena, including currents and fields, in nearby, adjacent superconductors. Josephson’s work enabled physicists to predict how properties like current and voltage would be induced across the space between two superconductors, and Clarke’s work built upon that idea. By separating two superconductors with a thin layer of non-conducting material — i.e., a Josephson junction — Clarke and his team were able to create a system that behaved as though it were a single quantum particle: one that filled the entire circuit.

This animation shows a diagram of a normal conductor with unpaired electrons (1), a superconductor with electrons teamed up into Cooper pairs (2), and a completed superconducting circuit behaving as a single quantum system. The animation shows a technical diagram for how the single quantum system architecture works, as designed by 2025’s Nobel laureates.

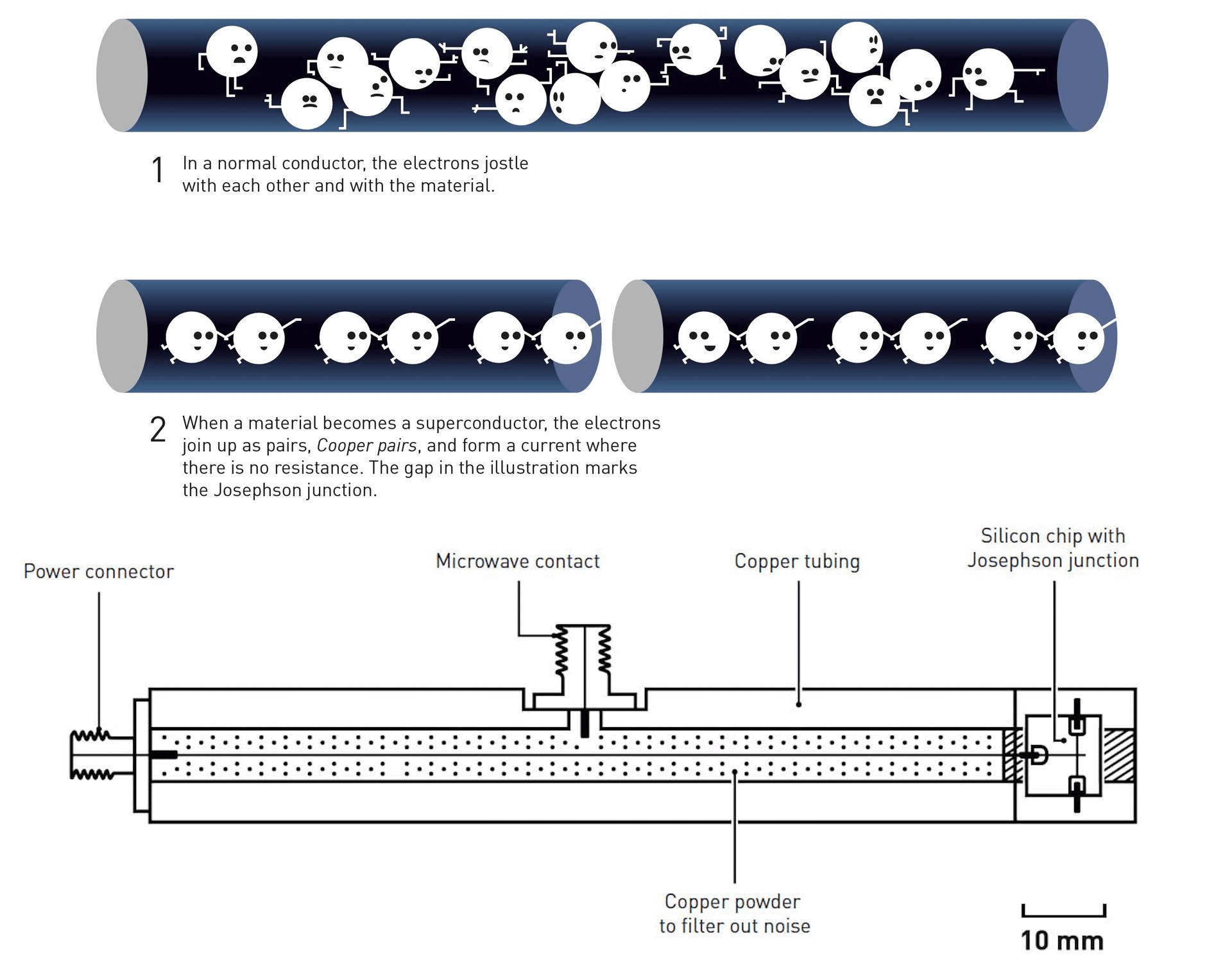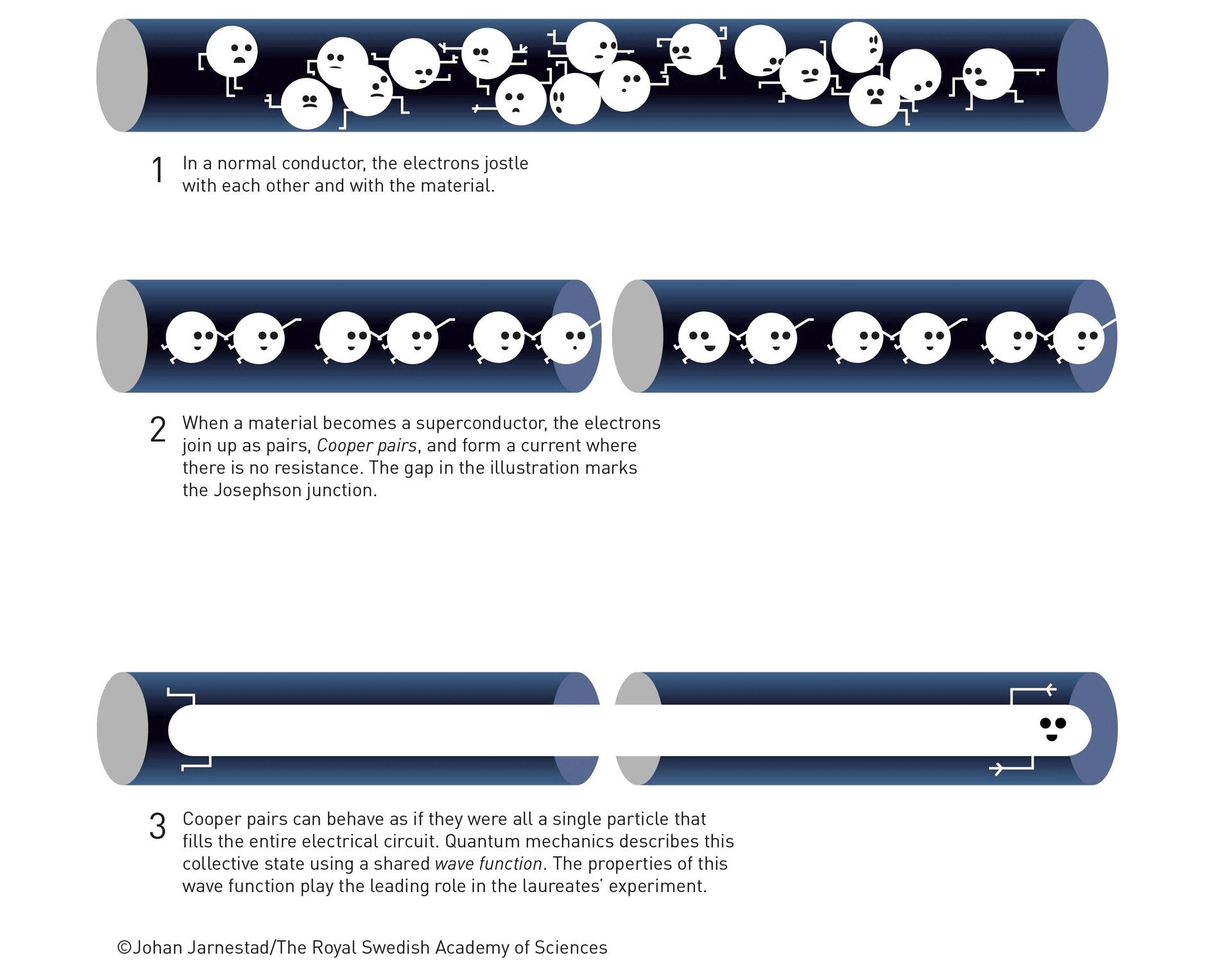
This macroscopic system behaves like a single particle in a number of ways: current is flowing within it, even with no external voltage applied to it, the same way a neutron has a magnetic moment or an electron has a property like “spin,” or an inherent angular momentum.

If you form a system like a neutral hydrogen atom — where an electron and a proton are bound together — there’s a 50% chance that they’ll form with the electron and proton both having their spins anti-aligned, and a 50% chance that they’ll form with their spins aligned. Whichever way they form, they can’t just transition freely from one configuration to the other; that’s forbidden by the rules of quantum mechanics, as the total spin of the system wouldn’t be conserved. However, it is possible to undergo a quantum tunneling transition (also known as a spin-flip transition) from the spin-aligned case to the anti-aligned case: the origin of the famed 21 cm hydrogen line.

Similarly, the macroscopic system that Clarke’s team pioneered finds itself initially in a state where the current flows without any voltage at all. The system, classically, is trapped in this state: as though it’s behind a barrier that it can’t cross. But the zero-voltage state, experimentally, showed that it can be escaped from, spontaneously transitioning to a state where voltage spontaneously appears: an example of macroscopic quantum tunneling.

In our familiar, classical world, the ability to go from a zero voltage state to a “voltage on” state requires energy, like the macroscopic flipping of a switch. But in the quantum world, such a transition can spontaneously occur through the phenomenon of quantum tunneling. The superconducting electronic circuit developed by 2025’s Nobel laureates was the first macroscopic system to exhibit this phenomenon.

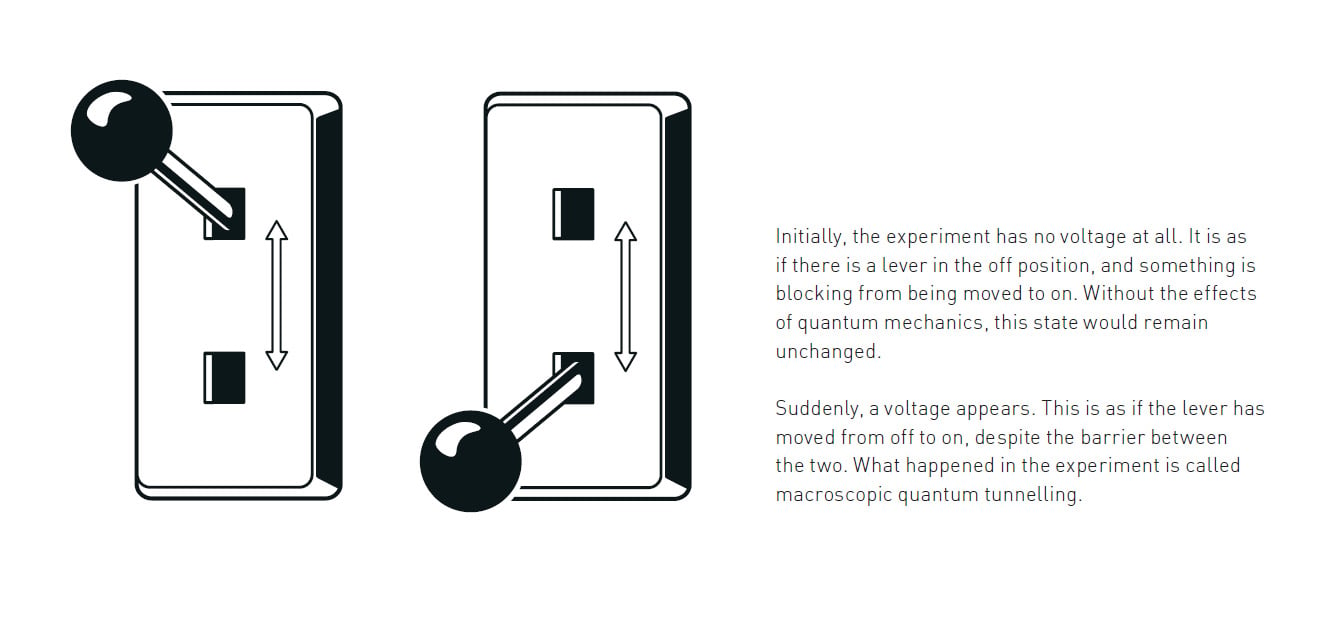
Even though the macroscopic system doesn’t have enough energy in it to overcome the barrier forbidding a transition from a zero-voltage state, the transition does indeed occur: through quantum tunneling. The next question to ask was what happens, then, if you try to impart certain specific amounts of energy into this macroscopic quantum system?

If the system, again, was like a hydrogen atom, you would expect that there would only be certain amounts of energy that the system was capable of absorbing: energies that corresponded to the precise amount needed to trigger the system’s transition from one quantum state to another. And, conversely, when the system de-excites, or transitions from an excited state to a lower-energy state, you would expect that only a series of quantized energy transitions could occur, just as the absorption and emission lines governing the Lyman, Balmer, and Paschen transitions (among all the others) are the only allowable energy transitions allowed for hydrogen.

For this macroscopic, superconducting electronic circuit, it would exhibit quantum behavior if and only if a certain series of energy amounts could be absorbed or emitted. Furthermore, the probability of having a spontaneous quantum transition should be dependent on the total amount of energy in the system at the time: higher-energy states should exhibit a greater probability of quantum tunneling than lower-energy states.

Just as a radioactive atomic nucleus can exist in configurations with different energetics, affecting the probability of a decay event occurring, so too can the macroscopic, superconducting electronic circuit systems that exhibit inherently quantum behaviors. This was another demonstration of the power of superconducting electronic circuits to behave as macroscopic quantum systems, and to tunnel from one energy state to another.

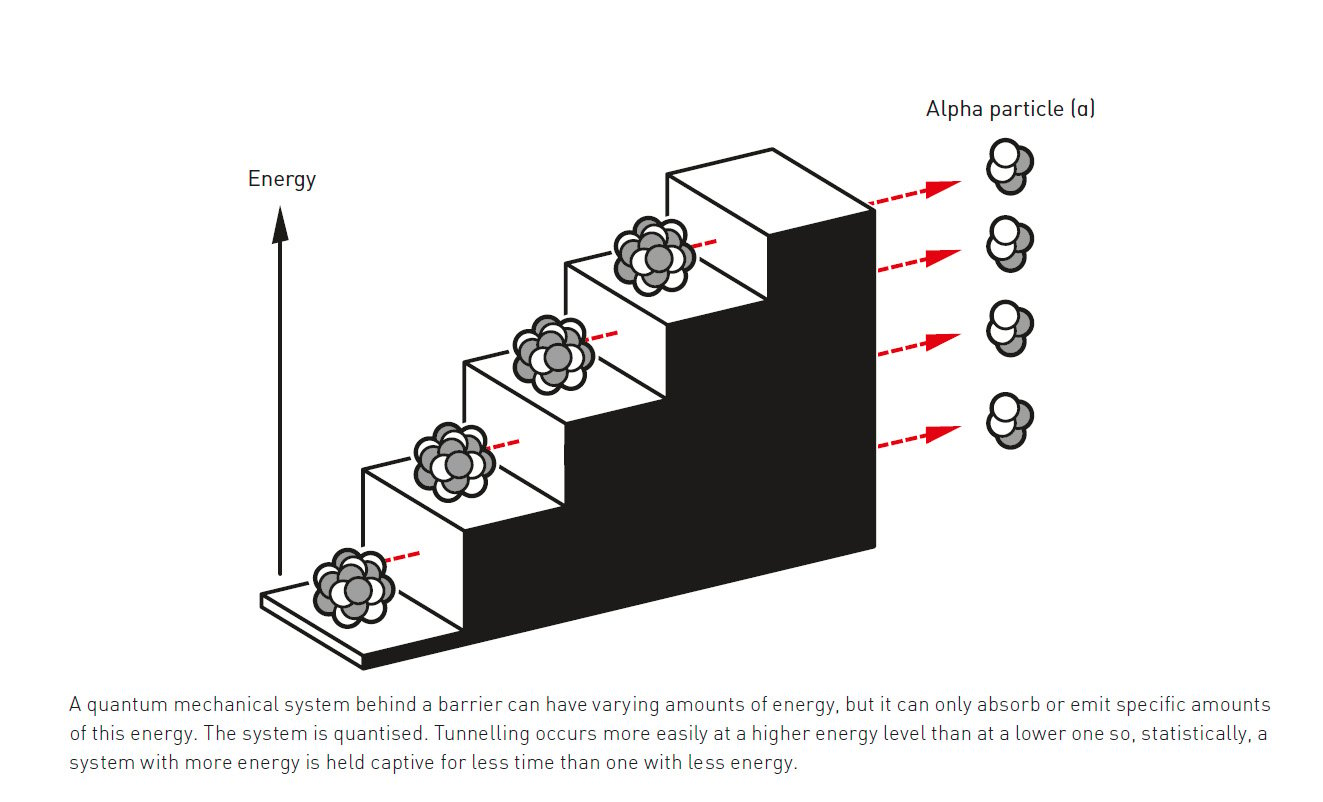
Indeed, this superconducting electronic circuit does have quantized energy levels, only emitting or absorbing energy in specific quantities. This was a remarkable advance: showing that an enormous, macroscopic system, one composed of quintillions of particles, including many trillions of electrons flowing through the superconducting circuit, can be described by a single wavefunction. That wavefunction, in turn, dictates the probability of observing this quantum system in a specific state with certain properties, as well as the probability of a transition occurring — spontaneously, even if classically forbidden — through the process of quantum tunneling.

While there were previous quantum effects that had been demonstrated on macroscopic scales:

• lasers,
• superconductors,
• and superfluid liquids,

this was the first set of experiments that involved vast numbers of particles, all together, acting as a single quantum system. It’s like having, in many ways, an artificial, large-scale version of an atom, but one that still maintains a quantum nature: with quantized energy levels and the ability to tunnel from one state to the other.

Part of what makes this work truly Nobel-worthy, in the sense that it has the potential to transform our world, is a follow-on experiment conducted by John Martinis, who went on to become a professor at UC Santa Barbara: using the two lowest-energy states of these artificial, macroscopic atoms as a solid-state qubit. This architecture, the superconducting qubit circuit, is currently the foundation for the highest-performance quantum computers currently in existence.

This rendition of a Sycamore processor mounted in a superconducting cryostat illustrates how Google’s quantum computer looked prior to the release of its Willow chip. Although qubits offer some computational advantage over classical computers, there is nothing that can be fundamentally simulated on a quantum computer that can’t also be simulated on a classical one. The goal of quantum computing is to achieve Quantum Advantage: Quantum Supremacy for a useful, practical problem.

In fact, this is arguably what the Nobel Prize should be all about: pioneering, breakthrough technologies that arise from fundamental research that, over the subsequent years and decades, reshape the world that we live in. In addition to quantum computers, the phenomenon of macroscopic quantum tunneling also powers the specialized imaging technologies in ultra-low-field MRI machines, quantum circuits present in (classical) advanced computers, and innovations that have led to ultra-precise measurements across the sciences: from neuroscience to geophysics to meteorology.

According to Irfan Siddiqi, the chair of UC Berkeley’s physics department (and a former postdoc of Devoret’s):

“The fact that you can see the quantum world in an electrical circuit in this very direct way was really the source of the prize. They showed that a macroscopic circuit kind of behaved like a single atom. It had levels… That quantization of the energy levels is the source of all qubits. This was the grandfather of qubits. Modern qubit circuits have more knobs and wires and things, but that’s just how to tune the levels, how to couple or entangle them. The basic idea that Josephson circuits could be quantized and were quantum was really shown in this experiment.”

This year, 2025, was designated by the United Nations as the International Year of Quantum Science and Technology, celebrating 100 years since the initial development of modern quantum mechanics. It’s only fitting that this year’s Nobel Prize went to one of the greatest quantum achievements of all: designing a macroscopic system that behaves as a single quantum particle. Congratulations to John Clarke, Michel Devoret, and John Martinis; the world is a better, smarter, and more capable place because of your incredible contributions. Enjoy your well-deserved moment in the spotlight!